This is part 2 of the Hypersyn blog series. Visit part 0 to explore the other parts of the blog series. To read the whole Hypersyn blog series in PDF form with included references, visit arxiv.
A Merkle tree is a binary tree data structure used to securely verify the presence of values in a list, without having to provide every value of the list to another party. To construct a Merkle tree, every value is hashed via a cryptographic hash function, the transformed values are also known as leaf nodes. The leaf nodes are then hashed together to form parent nodes, also known as non-leaf nodes. This step is repeated until the root of the constructed binary tree is reached (see Figure 1.).
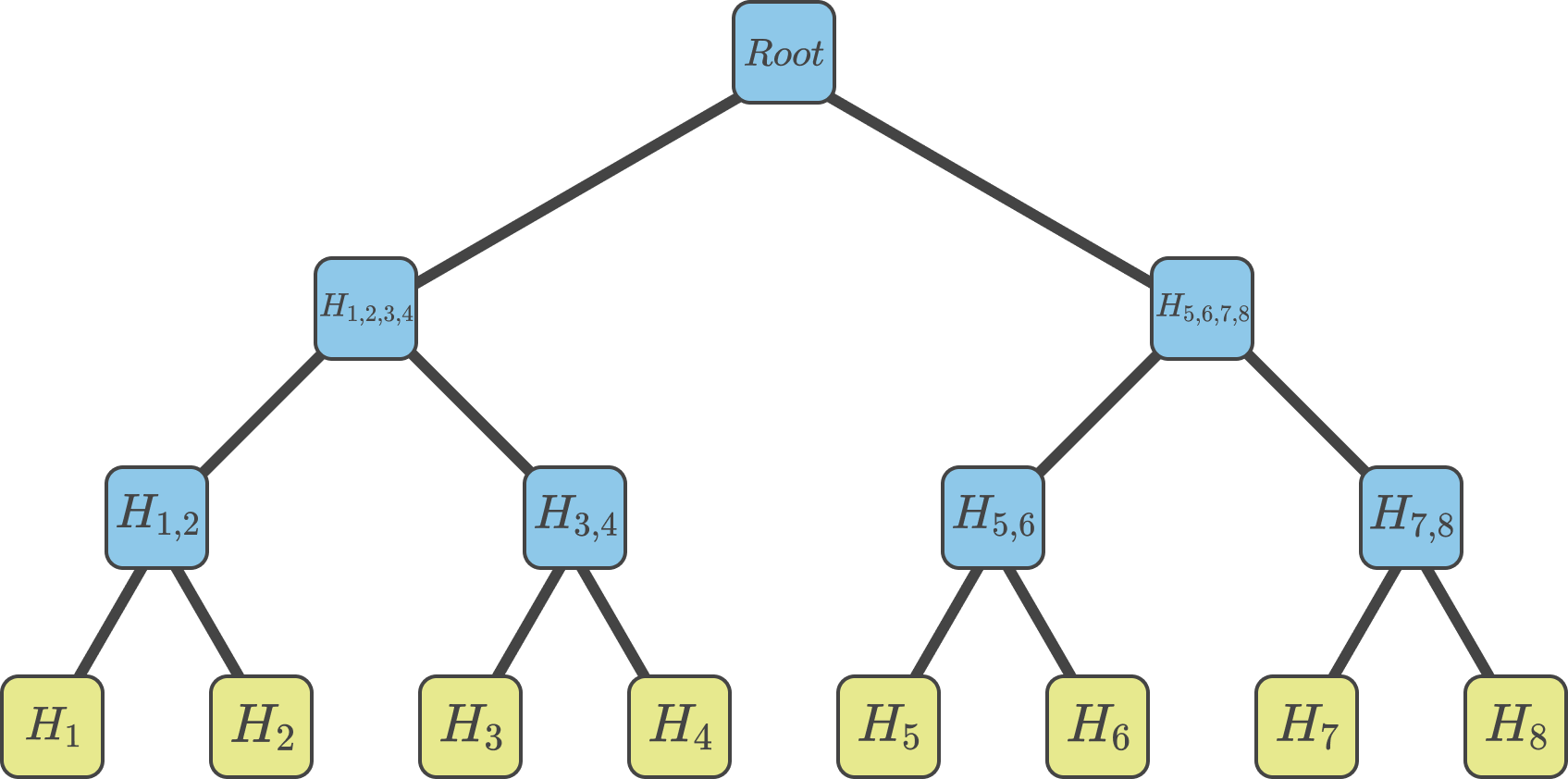
Figure 1. A depiction of a Merkle Tree. Leaf nodes are represented in yellow. Non-leaf nodes are represented in blue.
To verify that a value is present in the Merkle tree, a series of hashes (also known as the Merkle proof) is provided. By sequentially hashing the leaf node hash with the provided Merkle proof, the Merkle root of the original Merkle tree can be recreated (see Figure 2.). Note that recipients of a Merkle proof must already have a local copy of the Merkle root for a proof to take place. A node that receives a Merkle proof therefore, is able to verify if a value was part of the list of values that generated the Merkle root, by comparing their locally stored Merkle root, with the final hash generated by the provided Merkle proof. If the two hashes are equivalent, then the recipient of the Merkle proof knows that the provided value was indeed one of the leaf nodes in the original Merkle tree. This is also known as a presence proof. Instead of having to provide the whole list of $M$ values to another party to verify the presence of one specific value, Merkle trees allow to prove the presence of a value by providing only log(M) hashes.
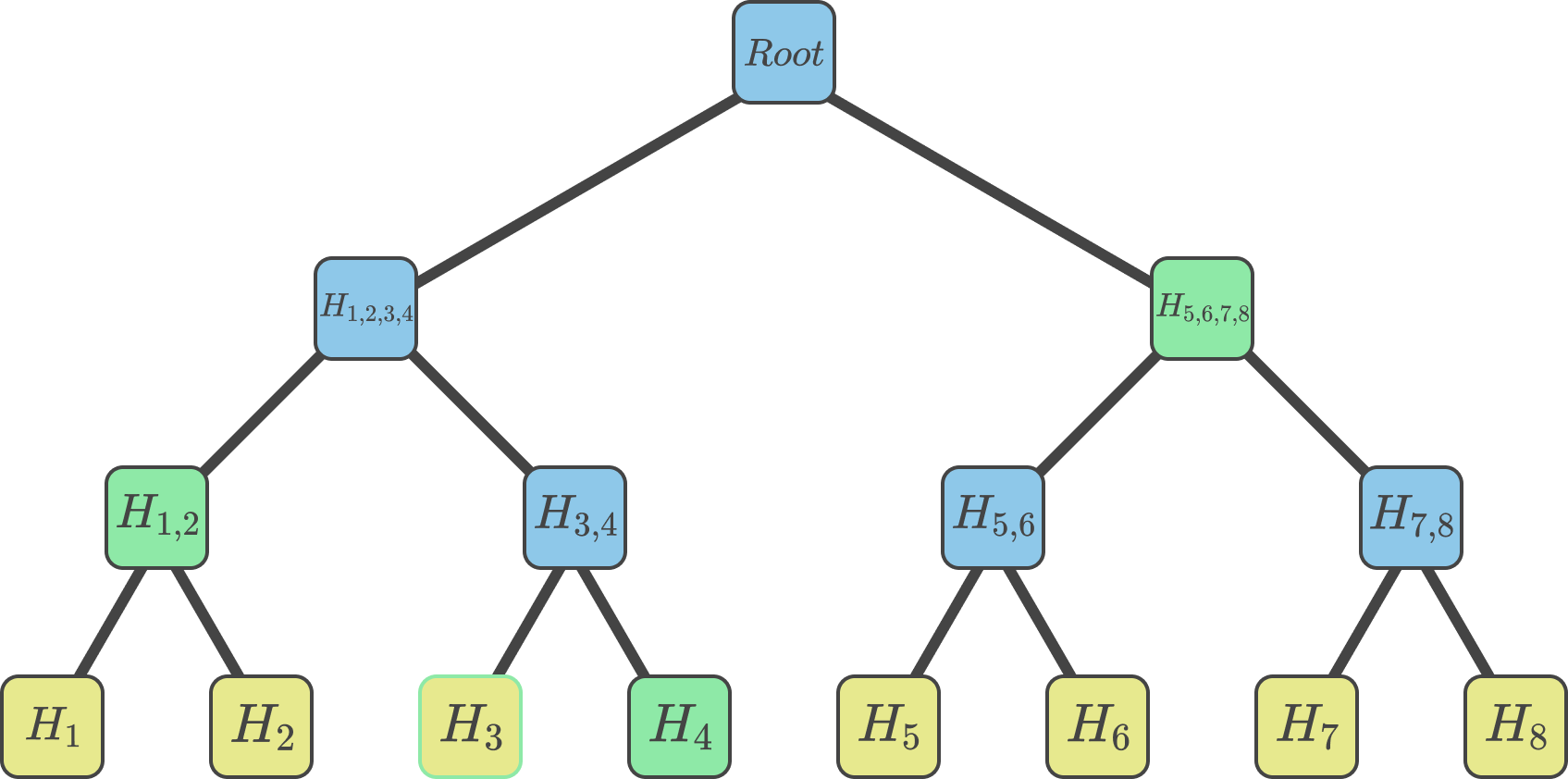
Figure 2. A depiction of a Merkle proof. To prove that H3 was present in the initial value list, one has to hash it with H4, then with H1,2, and finally with H5,6,7,8 (shown in green) to recreate the hash of the Merkle root.
While Merkle trees can provide presence proofs and perform value insertions with log(M) steps, they do not allow for efficient absence proofs, value updates, and value deletions. An absence proof is when a Merkle proof can show the absence of a value in a tree. In regular Merkle trees, absence proofs require leaf node sorting, while value updates and deletions require the re-computation of the whole tree, all of which are computationally expensive. The sparse Merkle tree (SMT) solves these issues by slightly redefining how a tree is constructed. In the SMT, one can both provide presence and absence proofs in log(M) steps on average, as well as perform insertions, deletions, and updates in log(M) steps on average.
Instead of constructing a Merkle tree bottom-up from a fixed set of values, SMTs start with an empty tree and sequentially add values to it. This is done by introducing the concept of empty nodes (a constant node with a fixed hash value), as well as by following a simple heuristic:
- To add a new value to the tree, begin from the tree root. If there is no value yet in the tree, let the tree root be the empty node.
- Let the path from a parent node to the left child node represent a zero, and the path to the right child node represent a one (see Figure 3.). Every value has a bit sequence (their cryptographic hash) that can be mapped onto the tree by sequentially choosing either the left side, or right side of a parent node, depending on the bits of the value’s hash. Go down the value’s path in the tree until a leaf node, or an empty node is reached.
- If an empty node is reached, substitute it with the new value. Taking Figure 3. as an example, inserting the orange value with ID 100 (at time step t2) will result in the substitution of an empty node with the actual value.
- If a leaf node is reached, create two child nodes and remap the values (by looking at the hashes of the values). If the values get mapped to the same child node, repeat the process and insert an empty node at the opposite child node. Taking Figure 3. as an example, inserting the yellow value with ID 011 (at time step t3) will result in the repositioning of the value with ID 010, as well as result in the creation of an empty node on the left side of the none-leaf node that was previously (in time step t2) the 010 leaf node.
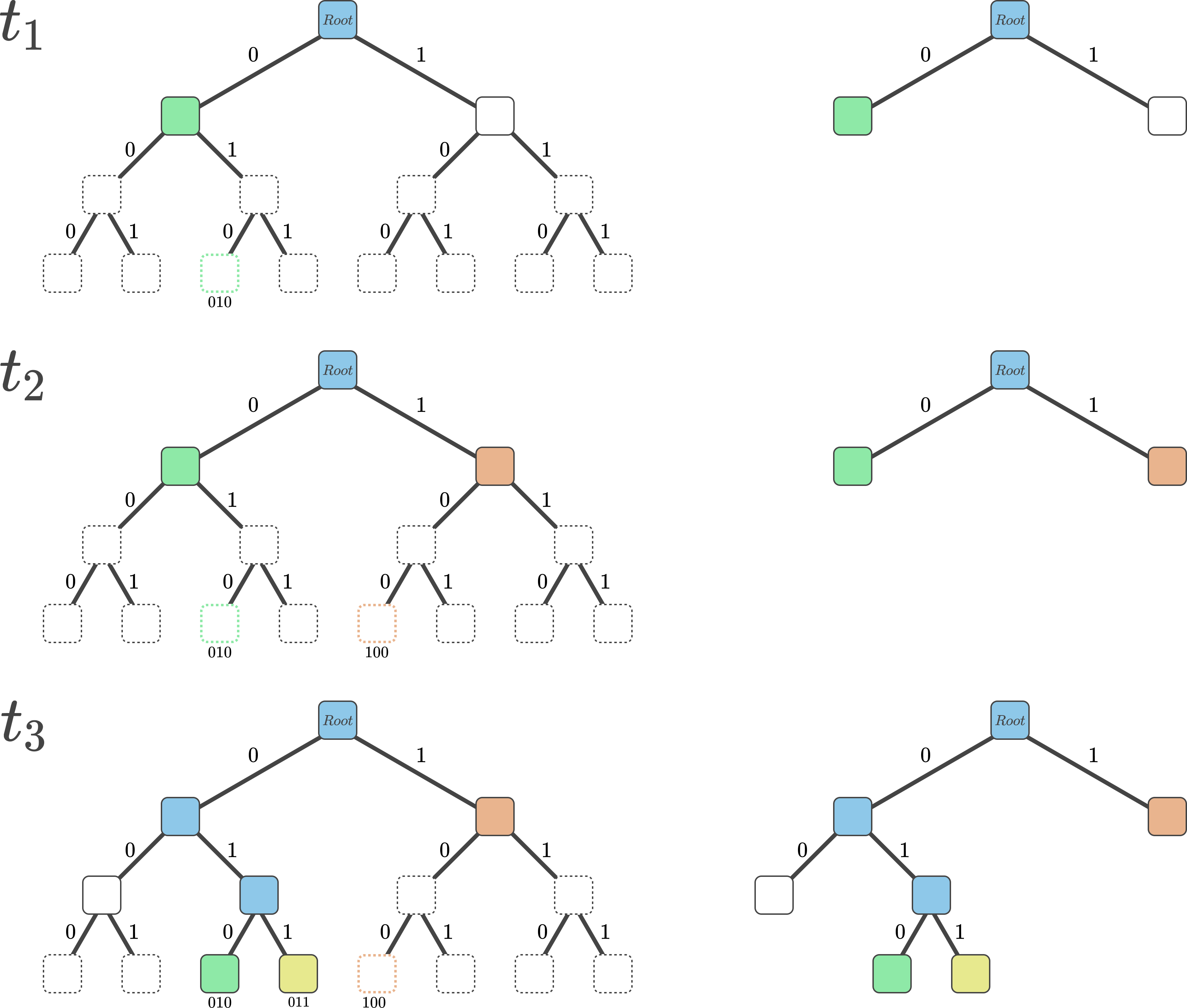
Figure 3. A depiction of a sparse Merkle tree. At every time step t a value is being inserted. Blue nodes represent non-leaf nodes. White nodes with full lines represent empty nodes. White nodes with dashed lines are not part of the SMT and serve to depict where value nodes in the tree would get mapped. The green (010), orange (100), and yellow (010) nodes represent the values, i.e. leaf nodes of the SMT.
Value deletions in SMTs work the exact same way as insertions, but in reverse. When removing a leaf node we move any sibling node up, until a parent node with another leaf node, or empty node is reached. Proving the presence of a value in SMTs is done the same way as in regular Merkle trees (see Figure 2. as reference), but surprisingly enough, so are absence proofs. To prove that a value was not part of a sparse Merkle tree, all one has to do is provide a regular Merkle proof, where the original leaf value of the proof represents the empty node value (a constant hash value). Taking Figure 4. as an example, to prove that the value with ID 001 (depicted with a yellow dashed line) is not part of the SMT, one simply has to provide the empty node, as well as the green leaf node and the orange leaf node to a recipient. By hashing the empty node value with the green node value and the orange node value, one recreates the original Merkle root and can therefore prove that any value that starts with 01 cannot have been part of the tree.
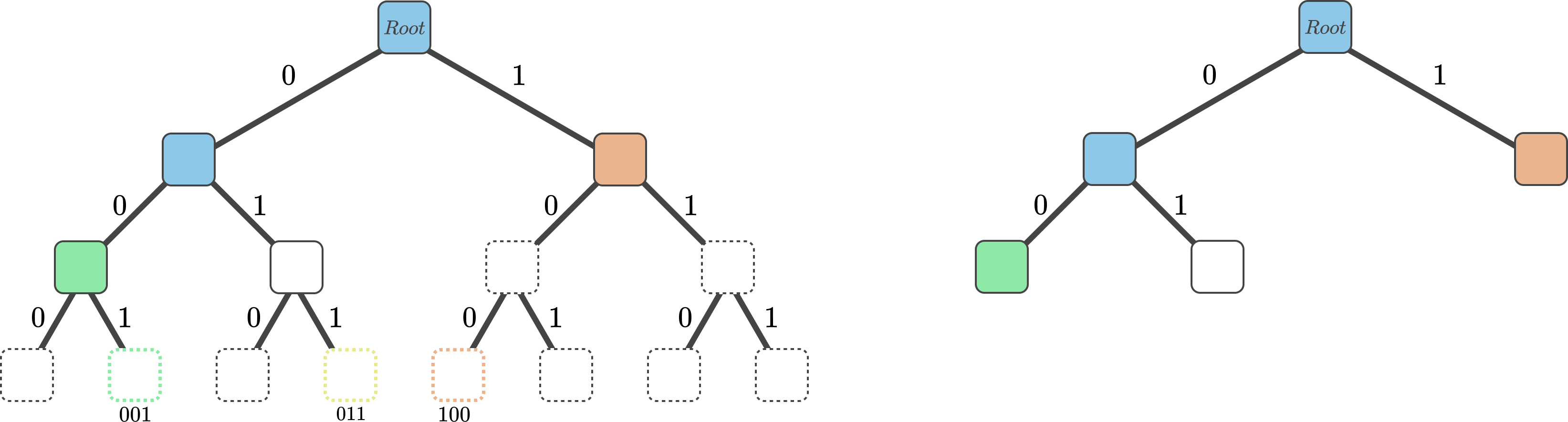
Figure 4. A depiction of a sparse Merkle tree. the value with ID 011 was never inserted into the SMT. One can show this by generating an absence proof.
In agent-centric protocol designs, nodes usually sign their Merkle roots with their private keys before sending it to peers. This is done to prevent malicious peers from forging another node’s Merkle roots. When the volume of requests on a node-basis is high however, that is, when a node has to update, insert, and/or delete many of its SMT values in a small amount of time, signing the Merkle root after every state change becomes costly. To overcome this scalability issue, nodes in Hypersyn can batch-sign a number of transactions (i.e. SMT state changes) by signing a single Merkle root and a counter, as long as the state changes have a partial order with each other (see part 3).